Hubungan dan Fungsi

Hubungan atau Relasi

Hubungan atau Relasi adalah suatu aturan yang memasangkan anggota-anggota dari himpunan satu anggota-anggota himpunan yang lain. Untuk menggambarkannya, dapat kita contohkan sebagai berikut:
Dalam sebuah keluarga kecil, terdapat 6 anggota yang terdiri dari Ayah (Budi), Ibu (Halimah), Anak ( Dony, Herman, Juan, Kalis, dan Sofie). Masing-masing anggota keluarga memiliki hobi sendiri – sendiri, Budi mempunyai hobi badminton, Ibu – merajut, Dony dan Herman – sepakbola, Juan dan Sofie – basket.

Dari kejadian di atas, kita dapat membuat relasinya dengan cara menentukan himpunannya terlebih dahulu.
Untuk daerah asal, kita ambil pemisalan dengan himpunan hobi atau A={badminton, merajut, sepakbola, basket}.
Untuk daerah kawan, kita ambil himpunan keluarga Bapak Budi atau B={Budi, Halimah, Dony, Herman, Juan, Kalis, Sofie}

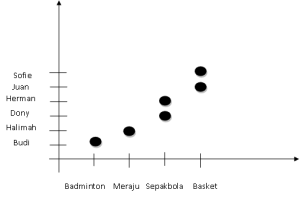
Relasi di atas dinamakan “Hobi Dari”. Cara membacanya adalah urut dari anggota paling atas, contohnya:

Badminton adalah hobi dari Budi, Merajut adalah hobi dari Halimah, dan seterusnya.

Cara menuliskan relasi dapat dinyatakan dengan 3 cara:

1. Diagram Panah

2. Himpunan Pasangan Berurutan

A ke B = { (Badminton, Budi), (Merajut, Halimah), (Sepakbola, Dony), (Sepakbola, Herman), (Basket, Juan), (Basket, Sofie) }

3. Diagram Cartesius

Fungsi

Fungsi adalah relasi khusus yang memasangkan setiap anggota (dari daerah asal/domain) dengan tepat satu anggota (dari daerah kawan/kodomain).Artinya, tidak ada anggota (dari daerah asal) yang memiliki kawan lebih dari satu dari (daerah kawan).
Dalam kehidupan sehari-hari, salah satu contoh dari fungsi adalah mata uang negara.

SIFAT FUNGSI

1. Injektif (satu-satu) apabila setiap dua elemen yang berlainan di A akan dipetakan pada dua elemen yang berbeda di B. Selanjutnya secara singkat dapat dikatakan bahwa f:A→B adalah fungsi injektif apabila a ≠  b berakibat f(a) ≠  f(b).

2. Surjektif (onto), misalkan f adalah suatu fungsi yang memetakan A ke B maka daerah hasil  f(A) dari fungsi f adalah himpunan bagian dari B, atau f(A)  c B. Apabila f(A) = B, yang berarti setiap elemen di B pasti merupakan peta dari sekurang-kurangnya  satu elemen di A maka kita katakan f adalah suatu fungsi surjektif atau “f memetakan A Onto B”

3. Bijektif (korespondensi satu-satu), misalkan suatu pemetaan f: A→B sedemikian rupa sehingga f merupakan fungsi  yang injektif dan  surjektif sekaligus, maka dikatakan “f adalah fungsi yang bijektif” atau “ A dan B berada dalam korespondensi satu-satu”.

JENIS FUNGSI

1. Fungsi Linear

Fungsi linear adalah suatu fungsi yang variabelnya berpangkat satu atau suatu fungsi yang grafiknya merupakan garis lurus. Oleh karena itu fungsi linier sering disebut dengan persamaan garis lurus (pgl) dengan bentuk umumnya f(x) = ax+b, dengan a sebagai koefisien dan c sebagai konstatnta
Langkah-langkah melukis grafik fungsi linier
a. Tentukan titik potong dengan sumbu x
b. Tentukan titik potong dengan sumbu y
c. hubungkan dua titik yang diperoleh sehingga terbentuk garis lurus

Contoh: Gambarlah grafik dari persamaan linear y=2x+4

Penyelesaian: 

2. Fungsi Kuadrat

Fungsi f: R→R yang ditentukan oleh rumus f(x) = ax2 + bx + c dengan a,b,c   ∈ R dan a ≠ 0 disebut fungsi kuadrat. Grafik fungsi kuadrat berbentuk parabola

Karakteristik Grafik Fungsi Kuadrat
Fungsi kuadrat  memiliki bentuk umum  . Dari bentuk aljabar tersebut dapat diilustrasikan sebagi bentuk lintasan lengkung atau parabola dengan karakteristik sebagai berikut.
Jika,
1.    a > 0, maka parabola terbuka ke atas
2.    a < 0, maka parabola terbuka ke bawah
3.    D < 0, maka parabola tidak memotong maupun menyinggung sumbu X
4.    D = 0, maka parabola menyinggung sumbu X
5.    D > 0, maka parabola memotong sumbu X di dua titik

Menggambar Grafik Fungsi Kuadrat
Langkah-langkah yang diperlukan untuk membuat sketsa grafik fungsi kuadrat  adalah sebagai berikut
a.    Menentukan titik potong dengan sumbu X, diperoleh jika y = 0
b.    Menentukan titik potong dengan sumbu Y, diperoleh jika x = 0
c.    Menentukan persamaan sumbu simetri 
d.    Menentukan nilai ekstrim grafik 
e.    Koordinat titik balik